Rise Time

Electronic devices do not respond instantaneously to changes when the input signal alters. For instance, when you switch on a light bulb, it takes a while for the bulb to achieve the highest luminescence. This delay is called rise time. Although it is desirable to have a long rise time, for instance, in the case of the light bulb to increase its lifetime, it is crucial to reduce this delay in high-speed electronics. Specifically, in quantum control problems, long delays result in distorted pulses that affect the fidelity of gate instruction.

To model such a finite delay of the electronic devices in the control stack, in the Qruise toolset, we have implemented a pseudo-device called RiseTime that mimics and simulates the delay specific to each electronic device. In their specification sheets, rise time characterises the time it takes for the output of a step function signal to reach from 20% to 80% of the maximum amplitude value, which is quite a standard range but can indeed vary. In the Qruise toolset, such behaviour is modelled by convoluting the pulse with a Gaussian filter. The difference between 80% and 20%, i.e. 0.6, defines the width of the Gaussian filter.

In this blog post, we will investigate the effect of rise time in a control stack constituting a single AWG device. Like always, let us define our flux line.

from qruise.toolset.libraries import components, hamiltonians

drive_line = components.Drive(
    name="flux_line",
    connected=["Qubit_0"],
    hamiltonian_func=hamiltonians.x_drive,
)

The RiseTime device receives two parameters. The first one is fraction which specifies the difference between the minimum and maximum amplitude percentages i.e. the value 0.6 implies the difference between 80% and 20% of the maximum amplitude. And the second parameter is rise_time which specifies how long it takes for a pulse to reach from the minimum amplitude fraction to the maximum amplitude fraction. The code block below shows how this is achievable in the Qrusie toolset.

from qruise.toolset.objects import Quantity as Qt
from qruise.toolset.generator.devices import OEMAWG, RiseTime, VoltsToHertz

# simulation resolution, different than the AWG sampling rate
sim_res = 1e11

awg_params = {
    "name": "AWG",  # given name of the device
    "sim_time": 20e-9,  # 20ns (pulse duration)
    "samp_rate": int(2.4e9),  # 2.4 GHz sample rate
    "waveform_granularity": 8,  # granularity of the AWG device
    "min_waveform_len": 16,  # shortest (in number of samples) waveform AWG can produce
}


risetime_devece_params = {
    "rise_time": Qt(value=450e-12, unit="s"),
    "fraction": Qt(value=0.6, unit=""),
}


stack_devices = {
    "AWG": OEMAWG(**awg_params),
    "RiseTime": RiseTime(name="RiseTime", **risetime_devece_params),
    "V2Hz": VoltsToHertz(
        name="V2Hz", V_to_Hz=Qt(value=1.0, unit="V/Hz")
    ),
}

stack_chain = {"drive_line": {"AWG": [], "RiseTime": ["AWG"], "V2Hz": ["RiseTime"]}}

The rise time is actually measured for a step function. Hence, it is natural to define the envelope of the pulse generated by the AWG to be a rectangular pulse.

from qruise.toolset.signal import pulse

t_gate = stack_devices["AWG"].sim_time

rect_params = {
    "amp": Qt(value=1.0, unit="V"),
    "t_start": Qt(value=0.0, unit="s"),
    "t_final": Qt(value=t_gate, unit="s"),
    "delta": Qt(value=0, unit=""),
}

rect_env = pulse.Envelope(
    name="rectangular",
    params=rect_params,
    shape=pulse.envelopes.rect,
)

But the rectangular pulse remains constant for the whole simulation since the gate time t_gate and the simulation time sim_time are equal. To generate a step-function envelope, we can add a delay to the envelope and only start generating it when we are half-way through the simulation time. This delay option is passed to the Instruction when we want to add the envelope to it. We create an identity instruction and assert that the envelope should only be generated for time stamps larger than t_gate / 2.

from qruise.toolset.signal import gates
from qruise.toolset.libraries import constants

instr = gates.Instruction(
    name="id",  # name of the instruction
    t_end=t_gate,  # duration of the instruction (pulse duration)
    channels=["drive_line"],  # to which channel the instruction (pulse) is applied
    targets=[0],  # the index of the target qubit (not relevant but mandatory)
    ideal=constants.Id,
)

instr.add_component(
    comp=rect_env, chan="drive_line", options={"delay": Qt(value=t_gate / 2)}
)

Then instantiate the Generator and produce the output pulse.

from qruise.toolset.generator.generator import Generator

generator = Generator(devices=stack_devices, chains=stack_chain)
generator.draw(instr=instr, resolution=stack_devices["AWG"].samp_rate)

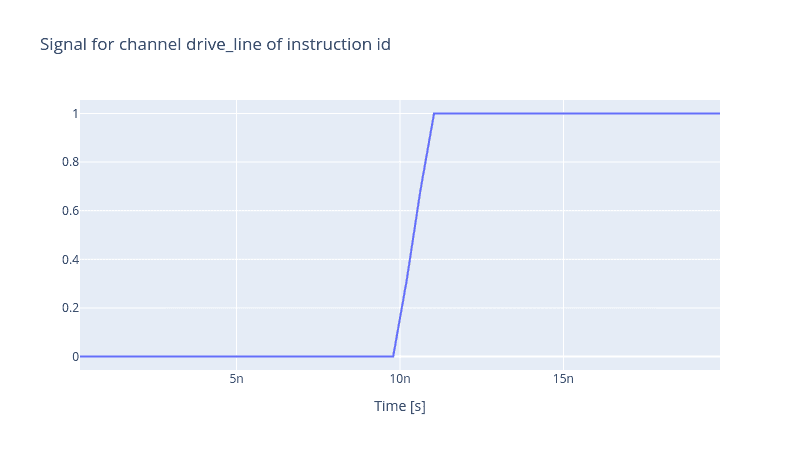
Actually, it is possible to measure the rise time by finding the indices of the 20% and 80% of the maximum amplitude. Once found, we extract the timestamps associated with these indices and subtract them consequently.

import numpy as np

signal = generator.generate_signals(
    instr=instr, resolution=8 * stack_devices["AWG"].samp_rate
)  # get the signal of the whole stack with a higher resolution compared to the AWG sample late

# get the timestamps
ts = signal.signal["drive_line"]["ts"]
# get the pulse generated by the RiseTime device
output_pulse = signal.signal["drive_line"]["signal_stack"]["RiseTime"]["inphase"]
# get the index of 20% of the maximum value
ind_2 = np.where(output_pulse.numpy() < 0.2)[0].max()
# get the index of 80% of the maximum value
ind_8 = np.where(output_pulse.numpy() > 0.8)[0].min()

risetime = (ts[ind_8] - ts[ind_2]).numpy() / 1e-12
print(f"Rise time of {risetime: .2f}ps")

Rise time of  468.75ps

The value is slightly different from the actual value 450ps we set earlier when we defined the RiseTime object, but this is due to the discretisation of time when we set the resolution of the Generator. The finer the simulation resolution is, the more precise the resulting rise time will be.