Improving gate fidelities in quantum processing units (QPUs) requires effective suppression of decoherence. Decoherence arises from environmental noise, and understanding this noise is crucial for mitigation. Quantum Noise Spectroscopy (QNS) is a valuable method for this, enabling the qubit to act as a noise spectrometer. By measuring the qubit's response to specially designed control sequences, QNS helps identify and target specific noise features, aiding in the development of tailored decoherence suppression strategies.

Various control schemes have been used to perform QNS, tailored to the spectral properties of the noise and the frequency range of interest, as summarised in the table below. Over the past two decades, these schemes have been experimentally implemented across a variety of qubit platforms, including diamond nitrogen vacancy centres, nuclear spins, superconducting quantum circuits, semiconductor quantum dots, and trapped ions.

Method	Statistics of noise	Reconstructed spectral property	Reconstruction frequency range
Repeated Ramsey spectroscopy	Gaussian, Stationary	Dephasing noise power spectral density (PSD) and control field inhomogeneities	mHz to 100s of Hz
Dynamical decoupling QNS	Gaussian, Stationary	Dephasing noise PSD and control field inhomogeneities	few Hz to 10s of MHz
Non-Gaussian Dynamical decoupling QNS	Non-Gaussian, Stationary	Higher orders spectrums of dephasing noise and control field inhomogeneities	few Hz to 10s of MHz
Spin-locking QNS	Gaussian, Stationary	Dephasing noise PSD	few Hz to 100s of MHz
Rabi spectroscopy	Gaussian, Stationary	Dephasing noise PSD and control field inhomogeneities	few MHz to over a GHz
T1 spectroscopy	Gaussian, Stationary	Transverse noise PSD	Around qubit frequency

In QruiseOS, we implement a method based on dynamical decoupling sequences to measure the power spectral density (PSD) of the dephasing noise experienced by the qubit. Specifically, we use a Carr–Purcell–Meiboom–Gill (CPMG) dynamical decoupling sequence which consists of a $[\tau - \pi - \tau]$ block repeated $N$ times between two $\frac{\pi}{2}$ pulses, where $\tau$ is the free evolution time. With careful consideration, we can correlate the noise PSD to a qubit observable measured under such a sequence.

Let’s understand it with an example involving the off-diagonal elements of the qubit density matrix, i.e., coherences as observables:

For a qubit subjected to surrounding noise and a control sequence, as $t \to \infty$, the coherence, $C(t)$, decays as

$C(t \approx 2 N \tau) = e^{-\chi(t)} ,$

where the attenuation function

$\chi(t) = \frac{1}{2\pi} \int_0^\infty |F(\omega, t)|^2 S(\omega) d\omega.$

Here, $S(\omega)$ is the PSD, which describes the effects of noise, and $F(\omega, t)$ describes the effect of the control sequence.

For a CPMG sequence,

$F(\omega, t) \approx \frac{4t}{\pi^2}\sum_{l = 0}^{\infty} \frac{1}{(2l+1)^2} \delta (\omega - \omega_l),$

which leads to the attenuation function

$\chi(t) = \frac{4 t}{\pi^2}\sum_{l = 0}^{\infty} \frac{1}{(2l+1)^2} S(\omega_l),$

with $\omega_l = \frac{l \pi}{2\tau}$.

As we can see from the equation above, a CPMG sequence with a specific free evolution time, $\tau$, makes the qubit sensitive to specific noise frequencies determined by $f_l = \frac{\omega_l}{2\pi} = \frac{1}{4\tau}$ and its harmonics, allowing us to directly observe their impact via qubit observables, such as the coherence. By repeating the sequence for different values of $\tau$, it’s possible to reconstruct the full noise PSD of the qubit.

If shape of the PSD allows, we can simply ignore the impact of harmonics (truncating the above series to $l=0$, called single-delta approximation) and correlate the noise PSD at $\frac{1}{4\tau}$ one-to-one with the qubit coherence. This provides an estimate of the full PSD through

$S(\frac{\pi}{2\tau}) = -\frac{4 t}{\ln [C(t)]\pi^2}.$

However, for general PSDs, to properly account for the impact of harmonics, more sophisticated analysis methods are required. In QruiseOS, we provide various analysis methods depending on the shape of the PSD.

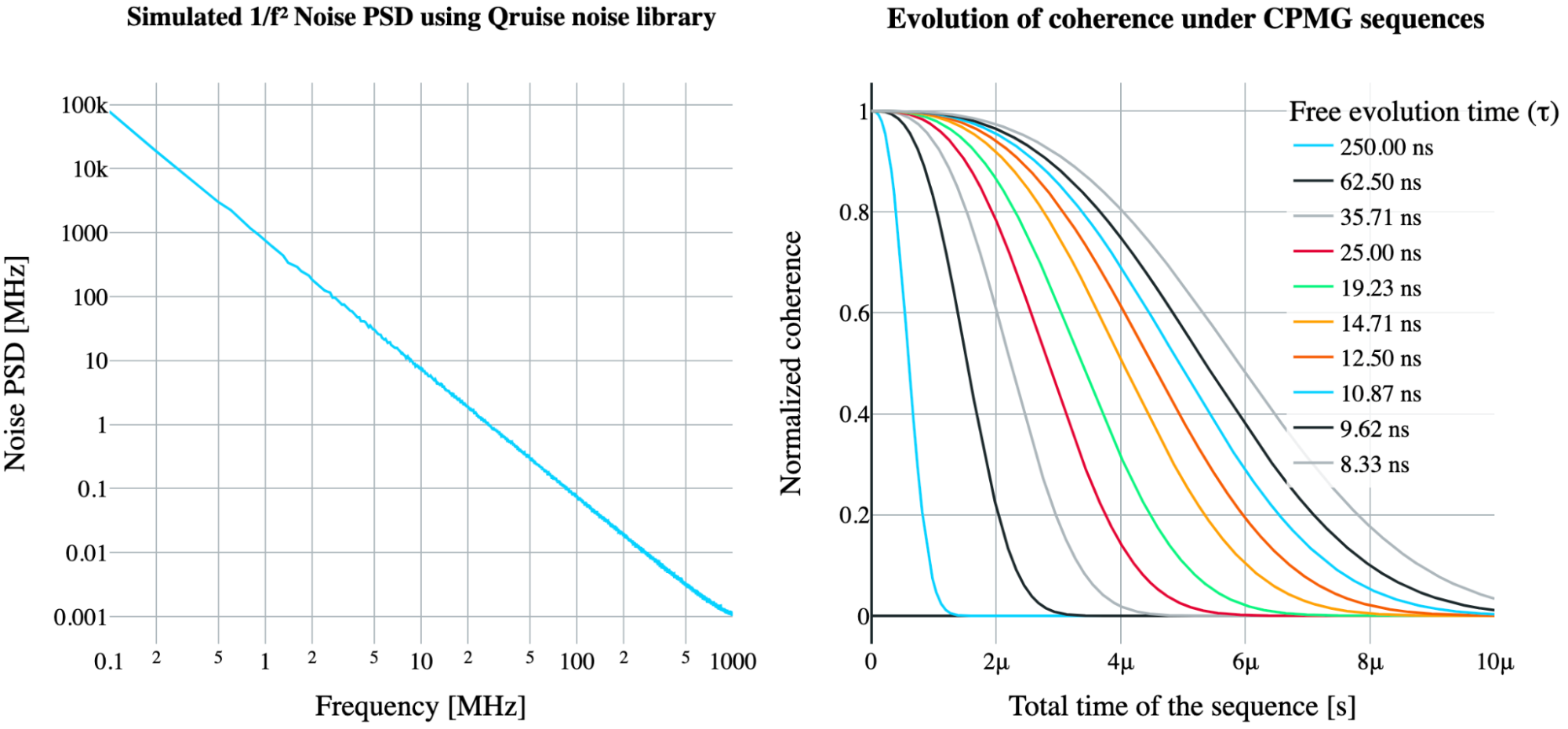
Let’s see QNS in action by estimating the noise PSD of the $\frac{1}{f^b}$ type, which is ubiquitous in solid state QPUs.

We use a qubit longitudinally coupled to a stochastic process as a noisy QPU. To generate stochastic processes following a specific PSD, we use the Qruise Noise Library, which supports the generation of an extensive class of Gaussian and non-Gaussian noise processes. We then subject the qubit to CPMG sequences with various free evolution times. In the figure below, you can see the simulated coherence for various free evolution times (right) and the corresponding noise PSD (left). The decay of coherence assumes a stretched exponential shape as expected for noise PSDs of the $\frac{1}{f^b}$ type. If $b=$ 1, the decay assumes the well-known Gaussian shape.

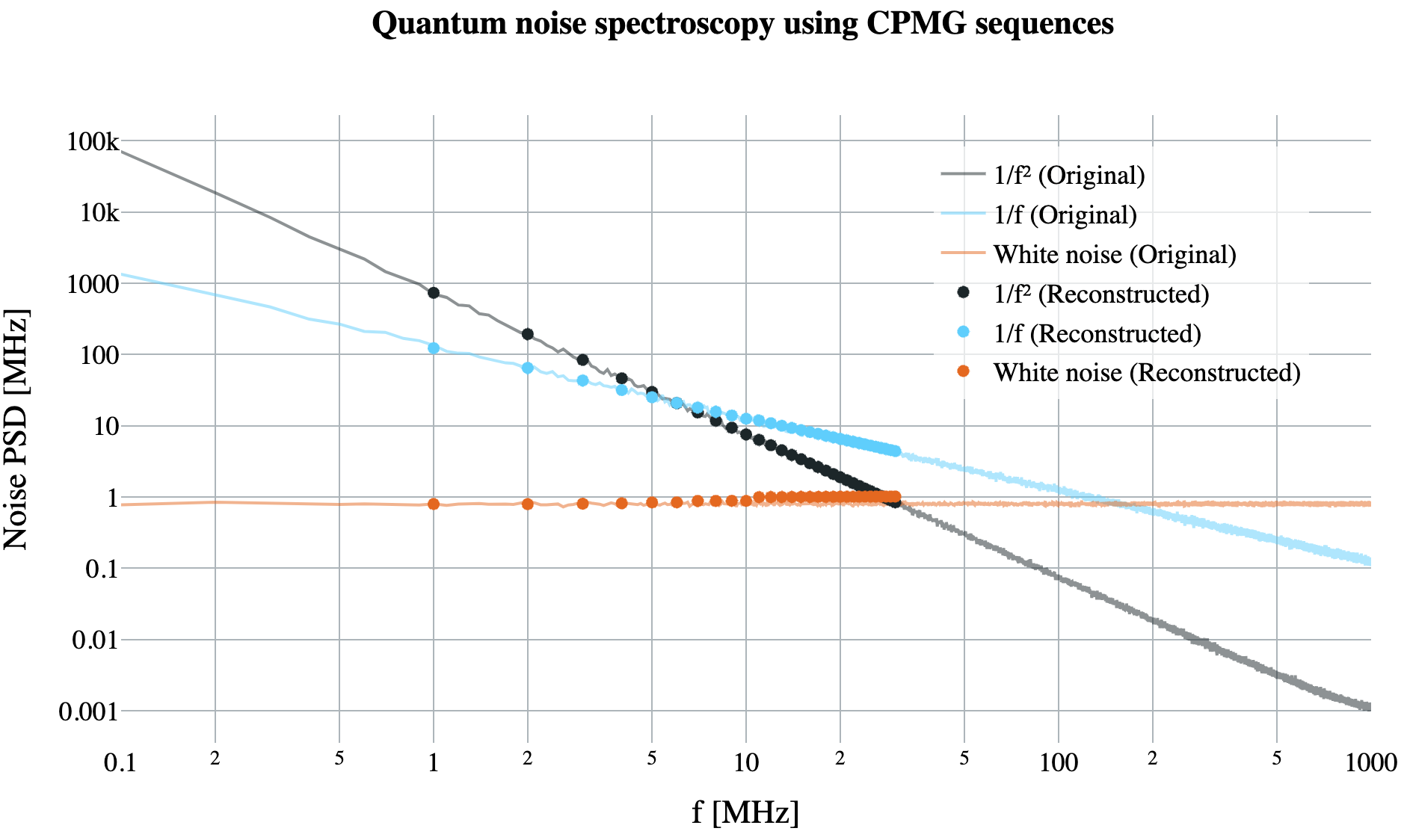
The coherence data, analysed using sophisticated methods like the Álvarez-Suter technique, accurately reconstructs the noise PSDs, confirming the efficacy of our noise identification and suppression strategies. You can see in the figure below the compelling comparison between the original and reconstructed PSDs, demonstrating our excellent capability to characterise surrounding noise and consequently shield and stabilise QPUs against it!

At Qruise we are constantly pushing the boundaries of noise estimation, so stay tuned for brand new features coming soon!